INTRODUCCIÓN


Resultado de imagen para sucesiones y series

Este tema se basa en el uso de los números para llegara determinada cantidad en un lapso de tiempo
o saber cuantos numero hay en determinado lapso de números sin la necesidad de escribir todos ellos solo con el  uso de formulas podemos llegar a esa cantidad buscada.
Es una secuencia lógica de números ya que puede ser creciente o decreciente. Las hay en progresión aritmética o progresión geométrica, la diferencia básica es que en la aritmética la razón de cambio entre un miembro y otro es la suma o resta de la misa razón, es decir:
0,1,1,2,3,5,8,13, es la serie o sucesión de Fibonacci, que se logra sumando los dos números anteriores, 0+1= 1, 1+1=2, 1+2=3, etc.
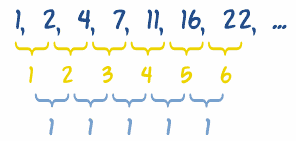
Imagen relacionada
Existen dos tipos de sucesiones numéricas, son las algebraicas y geométricas.
En la sucesión geométrica el número siguiente de la sucesión se logra por multiplicar o dividir la razón de cambio.
En cualquier caso la razón de cambio es constante y no puede variar, a menos que el cambio de la razón también corresponda a una sucesión, así podríamos tener una sucesión dentro de otra sucesión.
Una sucesión numérica se formaliza como una aplicación de los naturales en los reales, es decir :
\begin{matrix} u:& \mathbb{N} & \to & \mathbb{R} \\ & n & \to & u_n \end{matrix}
que escribiremos simplemente como \left\{{u_n}\right\}_{n \in \mathbb{N}} o, si se da por entendido que los subíndices son enteros, también vale \left\{{u_n}\right\}_{n \geq 0}.
El nombre que recibe la sucesión también puede hacer referencia a los valores que toma sobre los reales, así, si la imagen de u_{}^{} fuesen los racionales, es decir fracciones enteras del tipo \frac{a}{b}, \; b \neq 0, podemos llamarla sucesión de números racionales, y lo mismo para los irracionales, naturales, enteros, algebraicos, trascendentes, ... .
Una sucesión en \mathbb{R} es una enumeración de números reales , es decir una aplicación de \mathbb{N} en \mathbb{R}.

Comentarios

Publicar un comentario